
A supply chain is the entire network of individuals and organisations producing and delivering a product or service to the final consumer. It includes every step, from sourcing raw materials, manufacturing and assembling the product to transportation, warehousing, and finally, reaching the customer's hands.
Today, this multifaced network faces many disruptions, such as geopolitical tensions, economic fluctuations, climate change and evolving regulations. Simultaneously, common goals transcend industries, including customer satisfaction, cost optimisation resilience and adaptation. Both challenges and goals demand innovative solutions, with supply chain optimisation emerging as a crucial factor in ensuring efficiency.
Brief overview of supply chain optimisation
Supply chain optimisation (SCO) is a complex field dedicated to managing the flow of goods and services from raw materials to the end customer in the most efficient and cost-effective way possible. SCO is the adjustment of a supply chain's operations that ensures it is at the peak of possible efficiency.
Top five challenges of supply chain optimisation:
- Demand forecasting: predicting customer demand accurately is crucial for optimising inventory levels, transportation possibilities and production schedules.
- Inventory management: balancing the cost of holding inventory with the risk of stockouts.
- Transportation optimisation: selecting the most efficient and cost-effective routes for transporting goods, especially with factors like traffic congestion and fuel prices.
- Supplier selection and management: finding reliable suppliers who offer competitive prices and quality.
- Collaboration and communication: efficient cooperation between all players in the supply chain.
To tackle these challenges, SCO employs data analytics, mathematical modelling, optimisation algorithms, artificial intelligence (AI), and machine learning (ML). These tools collectively empower businesses to navigate the dynamic landscape of global supply chains with precision.
AI and ML, in particular, emerge as powerful allies in the pursuit of supply chain efficiency. Leveraging AI development and machine learning services helps automate tasks, enhance forecasting accuracy, and enable real-time decision-making, ensuring businesses can stay agile and responsive in the face of evolving circumstances.
Optimising supply chain management through AI integration
AI plays a significant role in improving supply chain efficiency. It can be used in different areas of supply chain management.
- Enhancing visibility and transparency:
-
- Real-time data collection and analysis - providing real-time insights into inventory levels, shipment locations, and potential disruptions.
- Predictive analytics - AI can analyse historical data and external factors like weather forecasts or economic trends, potential disruptions, and maintenance needs.
- Optimising operations and decision-making:
-
- Inventory management - AI can optimise inventory levels by forecasting demand, considering lead times and seasonality patterns, and minimising costs associated with overstocking or understocking.
- Route optimisation - AI algorithms can determine the most efficient and cost-effective routes for transportation, considering factors like traffic conditions, fuel consumption, and schedules in a way of finding a balance between transportation and inventory costs.
- Warehouse automation - AI-powered robots can automate tasks like picking, packing, and sorting, improving speed, accuracy, and efficiency in warehouses.
- Resilience and risk management:
-
- Risk identification - AI can analyse data to identify potential disruptions or supply chain vulnerabilities, allowing companies to take pre-emptive measures to minimise their impact.
- Scenario planning - AI can simulate various scenarios like natural disasters or economic downturns, helping companies develop contingency plans to ensure business continuity.
- Fraud detection and prevention - AI can detect anomalies in order data and financial transactions, identifying potential fraud attempts and protecting companies from financial losses.
- Sustainability and customer experience:
-
- Enhanced sustainability - AI can optimise processes to reduce waste, minimise energy consumption, and optimise fuel usage, contributing to a more sustainable supply chain.
- Personalisation and customisation - AI can personalise the customer experience by tailoring product recommendations and offerings based on individual preferences and purchase history.
Let's explore how AI, in particular, plays a transformative role in reshaping the supply chain in the retail industry, illustrated by a real-world use-case.

Developing an intelligent supply optimisation system
Our client, a manufacturer of plumbing tools and equipment with distribution points all around the United States, needed help optimising the supply process.
The main struggle stemmed from the elevated experiences associated with transporting goods from factories in China to distribution centres in the US. The customer maintained numerous warehouses and sales points across almost every state. Thus, determining the optimal routing posed a non-trivial task.
In addition, it was crucial to consider the preferred transportation chain. Each product begins its journey in a shipping container from a Chinese seaport and travels the Pacific Ocean to reach a port in the United States, from where it continues its journey in a truck to the designated warehouse. Afterwards, the product awaits last-mile delivery to the targeted distribution point.
The customer wanted to have the following functionality:
- specify available warehouses;
- identify distribution points, with some automatically derived from historical data and others manually selected by the user;
- create a list of items along with their respective quantities;
- have a list of seaports.
Finally, the client expressed a wish to be able to compare various methods of packing goods within shipping containers, either with or without pallets. The outcome of the optimisation problem should yield the optimal transportation schedule and associated expense statistics.
But before we dive into use case details, we will quickly outline a fundamental mathematical concept that is used in the intelligent solution.
Integer Programming for supply chain efficiency
Integer (Linear) Programming (IP) is a mathematical optimisation technique used to find the best solution to a problem with linear relationships while considering that either some or all the variables must take integer (whole number) values. The general form of an IP problem is to maximise (or minimise) a linear objective function subject to a set of linear constraints, where some or all the decision variables must be integers.
The objective function is a linear combination of decision variables, and the constraints are linear inequalities or equalities that the variables must satisfy. The mathematical formulation of an IP problem can be expressed as follows:
Maximise: c_{1}x_{1} + c_{2}x_{2} + ... + c_{n}x_{n}
Subject to:
a_{11}x_{1} + a_{12}x_{2} + ... + a_{1n}x_{n} ≤ b_{1}
a_{21}x_{1} + a_{22}x_{2} + ... + a_{2n}x_{n} ≤ b_{2}
...
a_{m1}x_{1} + a_{m2}x_{2} + ... + a_{mn}x_{n} ≤ b_{m}
and
x_{1}, x_{2}, ..., x_{n} are integers.
Values x_{1}, x_{2}, ..., x_{n} are the decision variables, c_{1}, c_{2}, ..., c_{n} are coefficients in the objective function, a_{ij} are coefficients in the constraint equations, and b_{i} are constants.
Solving an IP problem involves finding the values of the decision variables that optimise the objective function while satisfying the linear constraints and the additional requirement that the variables must be integers. IP problems are commonly used in various fields, including operations research, logistics, manufacturing, finance, and telecommunications, where decision variables often represent quantities that must be whole numbers.
Integer Programming is a valuable tool in solving supply chain optimisation problems due to its ability to model complex decision-making processes involving discrete (integer) variables.
- The ways IP can be applied in the context of supply chain optimisation:
-
- Inventory management: IP can assist in determining optimal inventory levels for different products at various stages of the supply chain, by considering constraints like storage capacity, demand variability, and order quantities, IP models can find the best balance between holding costs and stockouts.
- Production planning: IP can optimise production schedules by considering factors such as production capacities, raw material availability, and demand forecasts. The model can help in determining the optimal quantities to produce for each product to meet demand while minimising costs.
- Routing and scheduling: IP models can be applied to optimise the overall structure of the supply chain network.
- Supply chain network optimisation: IP models can be applied to optimise the overall structure of the supply chain network.
- Demand planning: IP models can incorporate demand forecasting data to optimise production and distribution decisions while aligning supply chain operations to anticipated customer demand, reducing the risk of overstock or stockouts.
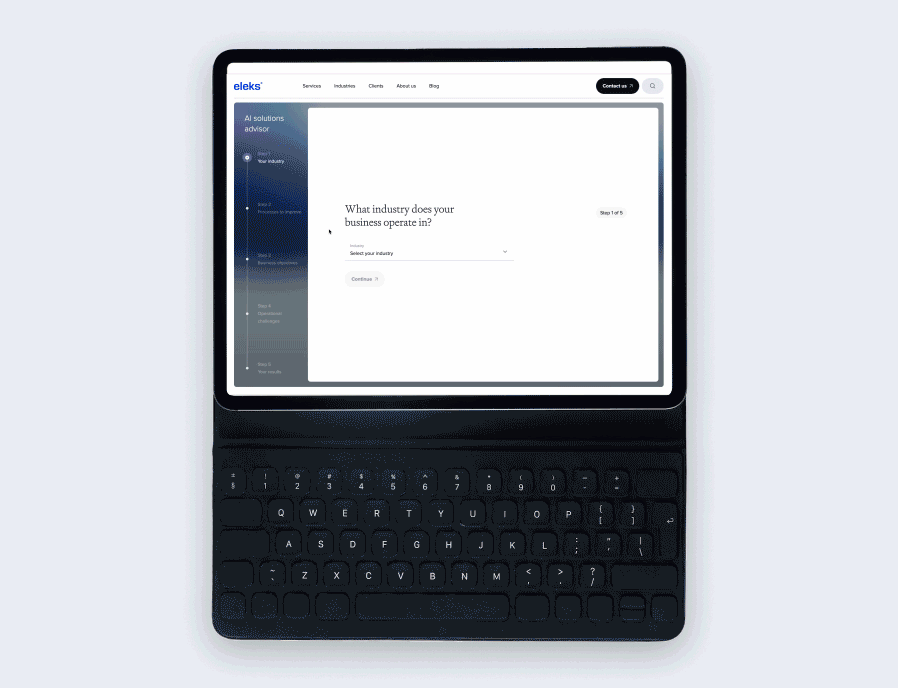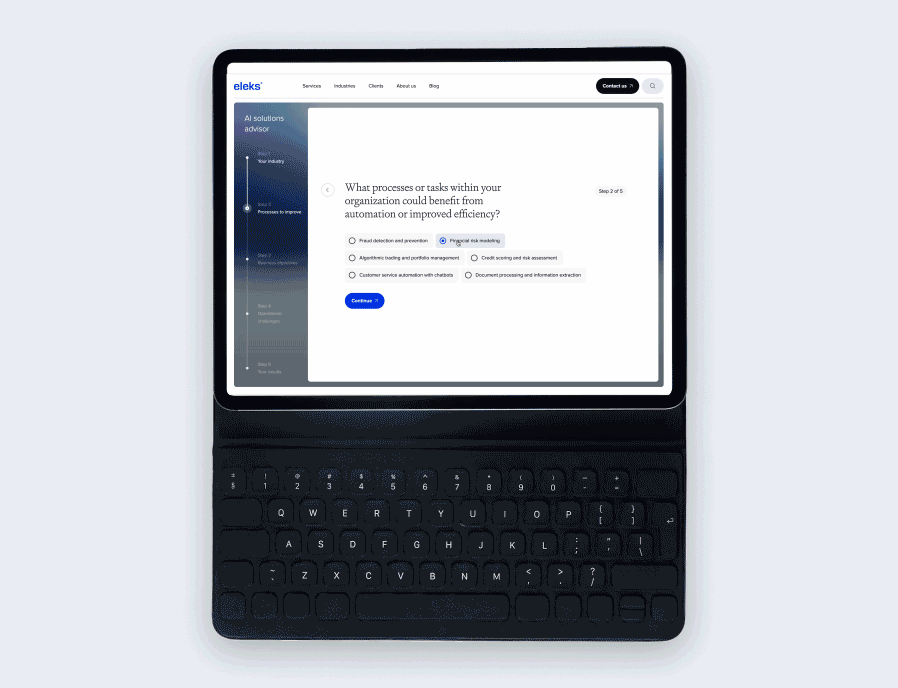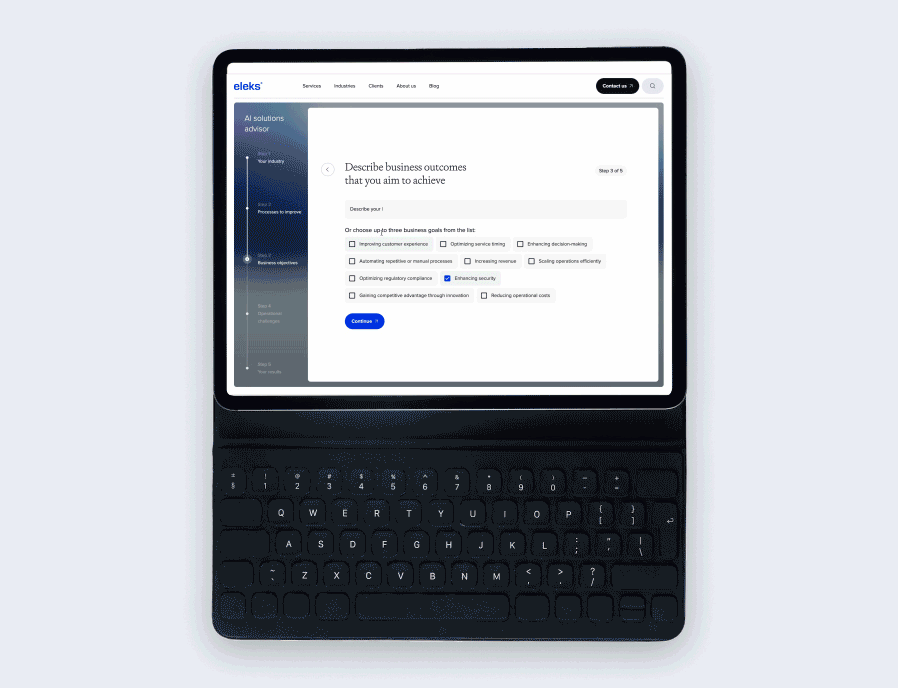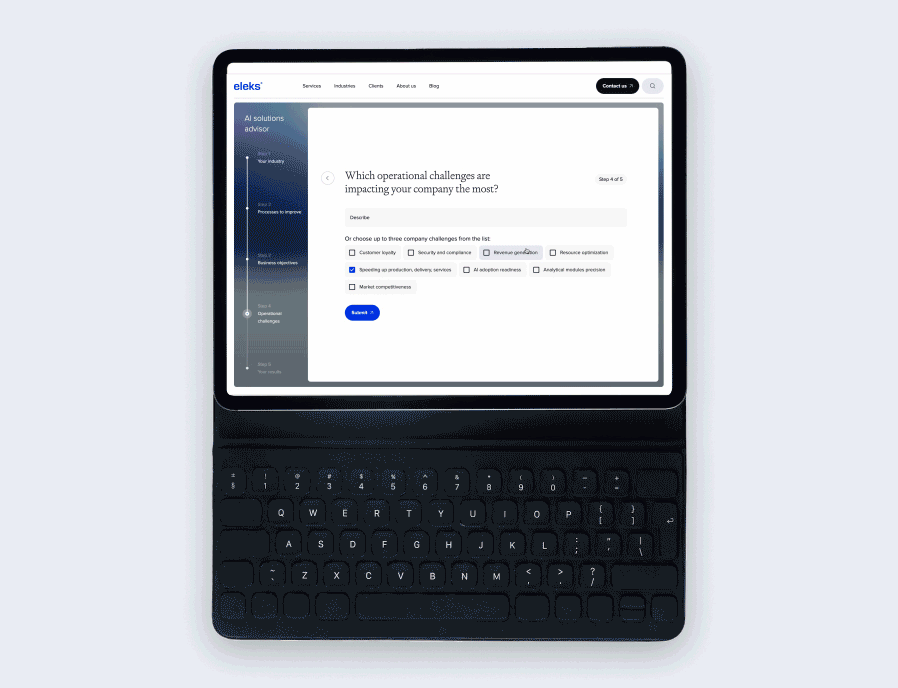
Enhancing supply chain logistics – ELEKS’ solution overview
To meet our client's requirements, we created a system that leverages the benefits of the Integer Programming technique, which optimises supply schedules, routes, and inventory levels for five kinds of items: ceramic sinks, toilets, bidets, gas valves, and bathtub mixers (corresponding HS codes are 6910.10.0030, 6910.10.0010, 6910.10.0025, 8414.90.1080, 7323.93.0080). The system comprises three main parts (or pages): configuration, simulation, and analytics. Each of them will be explained in the following paragraphs.
To ensure the confidentiality of data and application details, we anonymised names and real locations, creating a prototype for a straightforward demo application that illustrates the efficacy of AI in addressing optimisation challenges.
Configuration page
The user can select available warehouses, distribution points, and desirable seaports to take part in final optimised routing. Also, the client can specify desirable goods and their respective amount to be transported to their customers. The last thing is the date picker, in case delivery is planned. The system will calculate remains inventory at the delivery date based on forecasted demand and allocate planned shipments aligned with warehouse residuals. Clicking the 'optimise' button does all the magic! It sets optimisation tasks and launches its solution. After a few seconds, results can be observed on the remaining two pages.
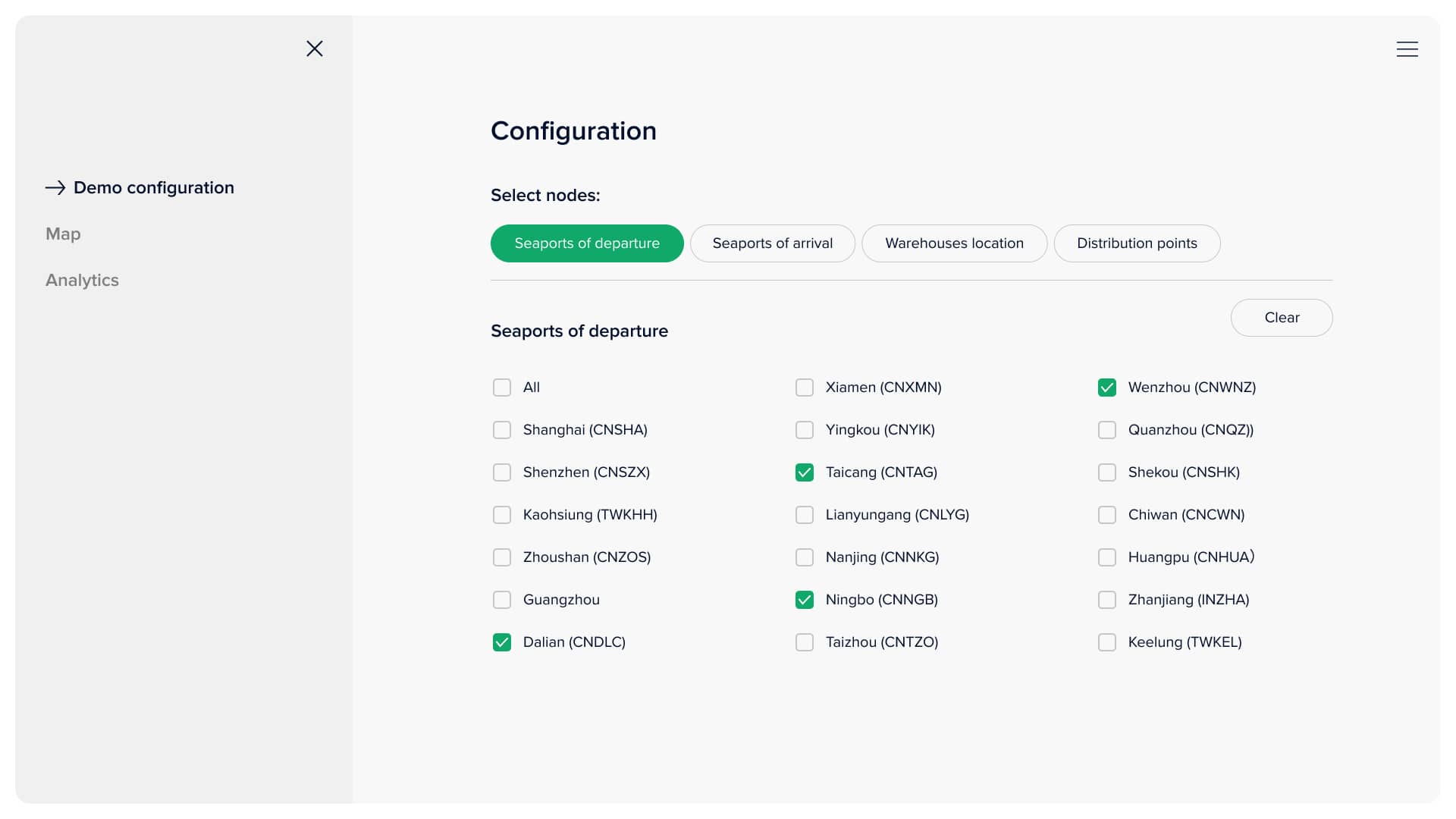
Selection of nodes to take part in optimisation process
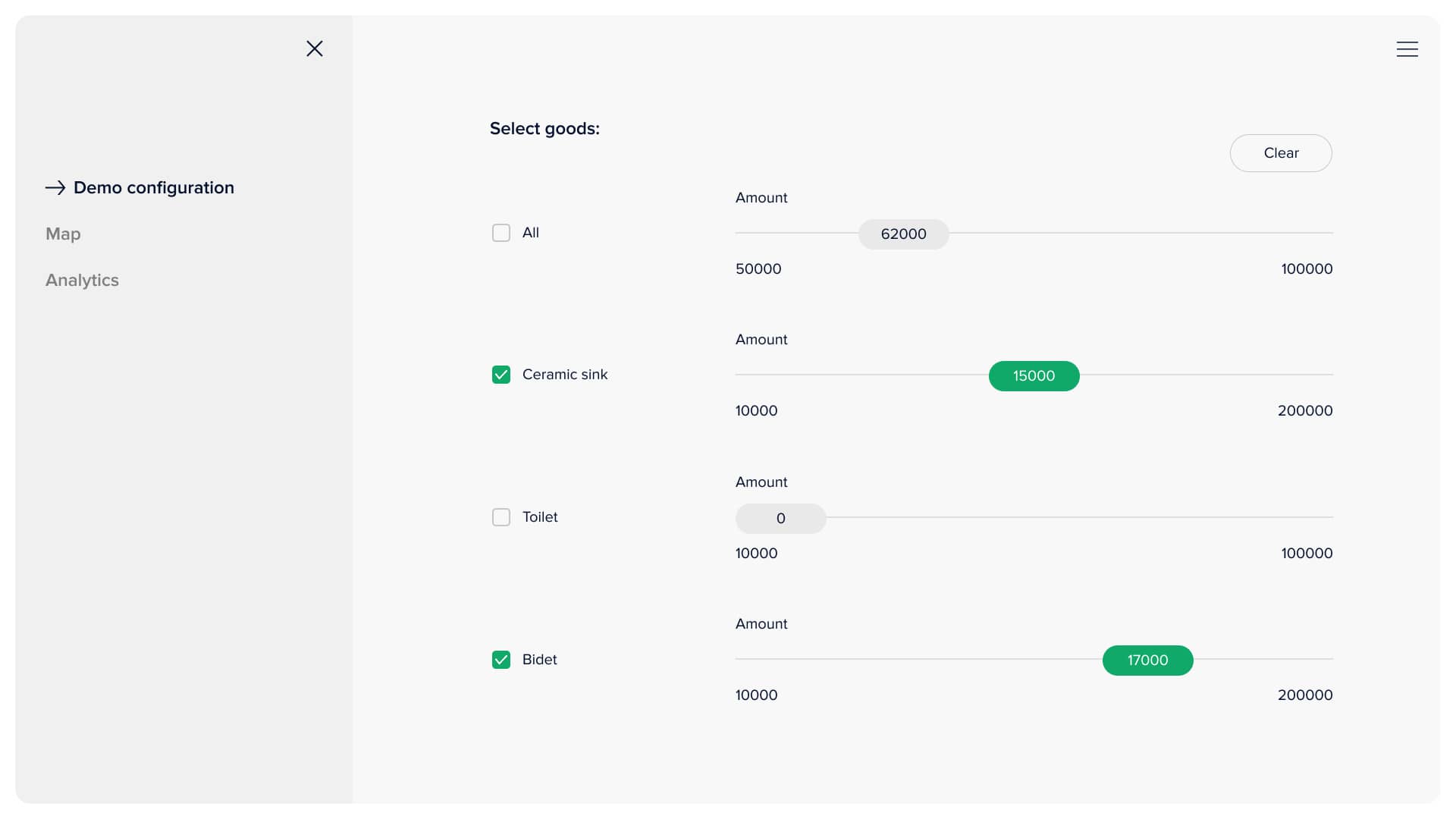
Goods selection
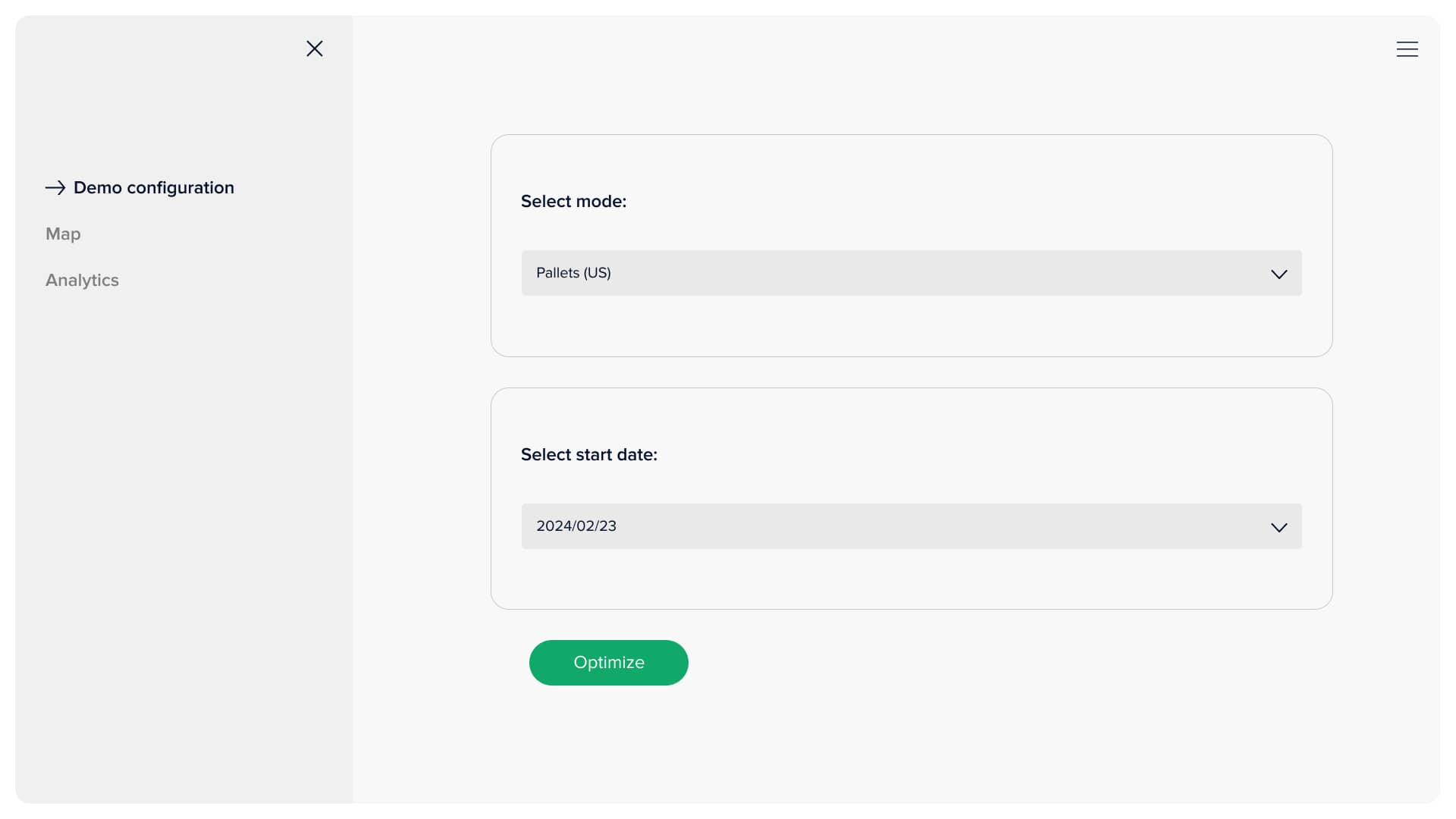
Mode and date selection
Simulation (map) page
This page offers the client the opportunity to view an accurate simulation of the proposed model's solution. In prior discussions, we deliberated on the suitable INCOTERMS for our client and reached a consensus on CFR. The customer can specify the number of hours for each step and press the corresponding button to see the state of the supply chain in this amount of time. First of all, there are five types of points: two for transport vehicles (ship and truck) and three for seaports (orange), warehouses (purple), and distribution points (green). The map is interactive, meaning the user can hover over any point or connection and see the information related to that object. For example, blue lines connecting warehouses and distribution points show the last-mile delivery plan and contain information about how much each good is delivered daily. If the user hovers over the ship, the information about its capacity, container types, loaded amount of each good, and routing are displayed.

Visualisation map
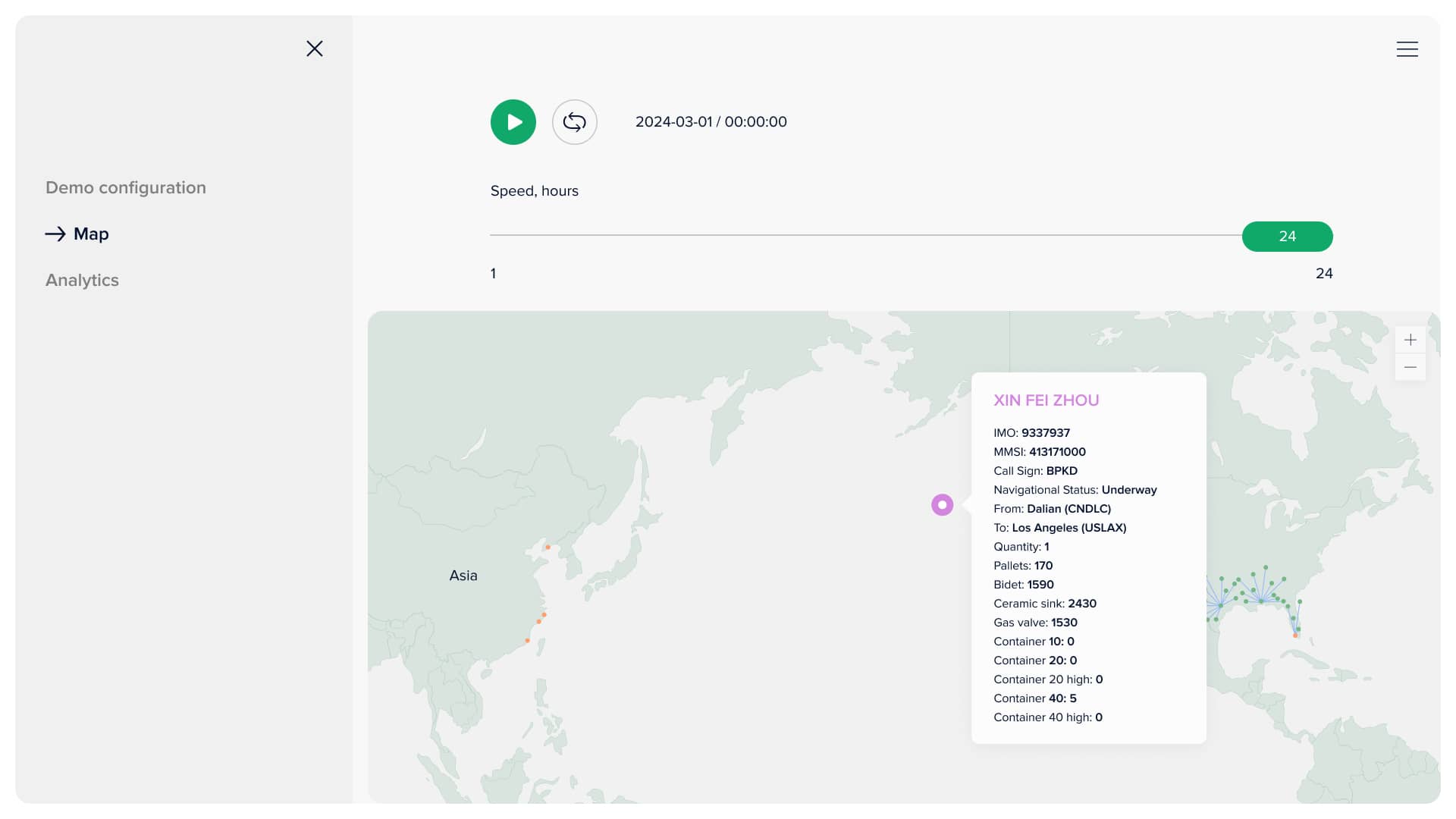
Ship information
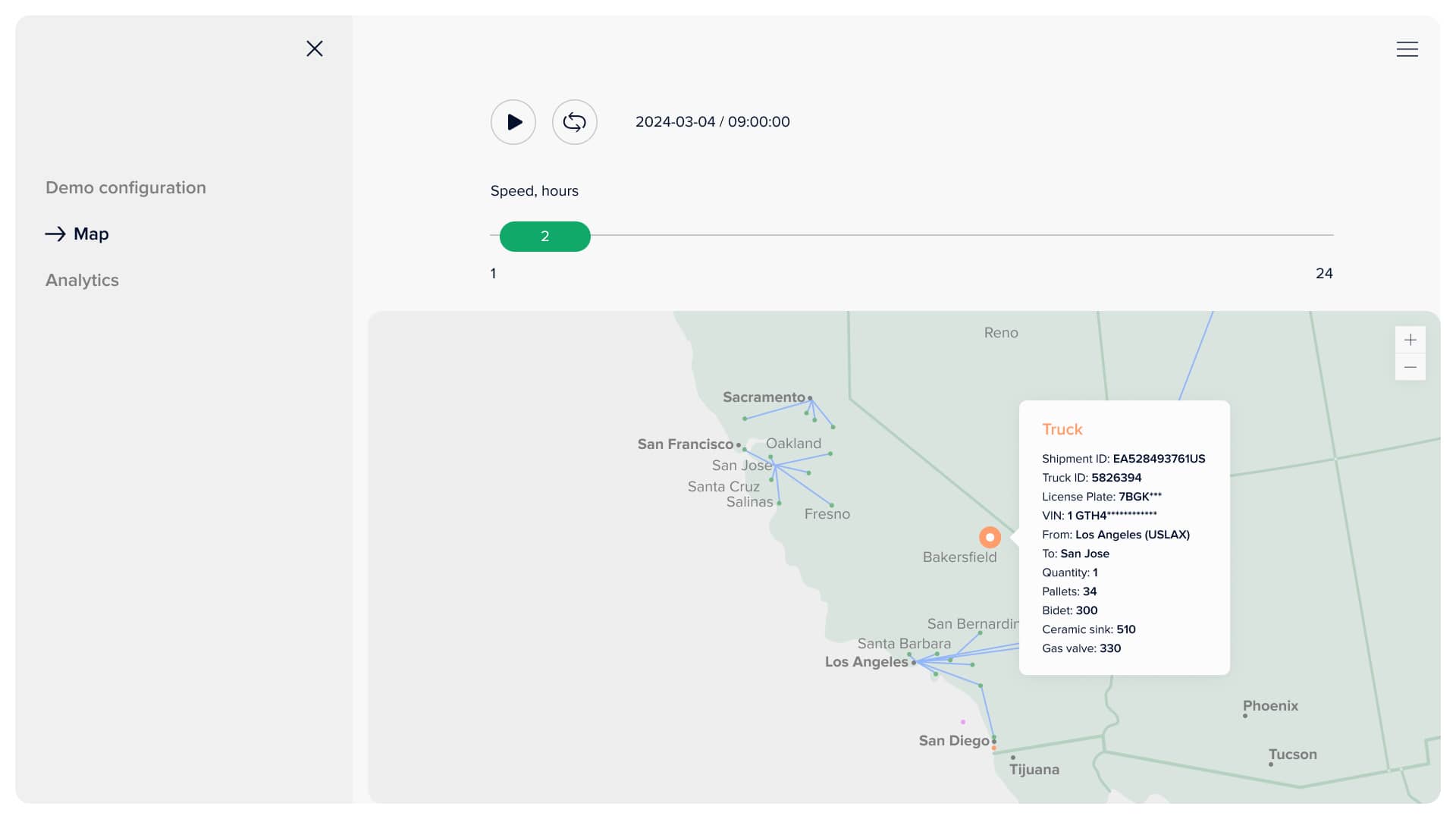
Truck information
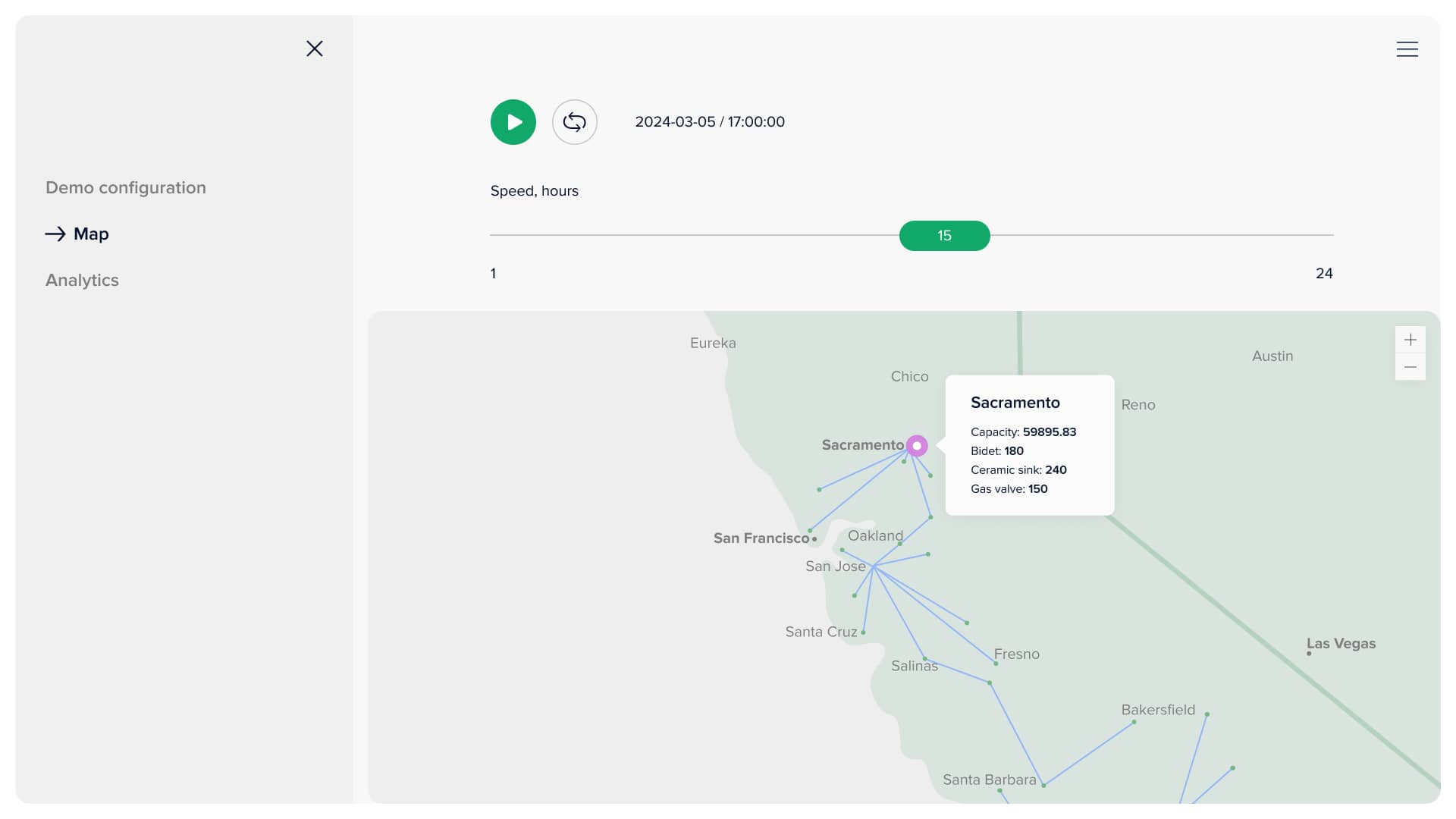
Warehouse data after truck arrival
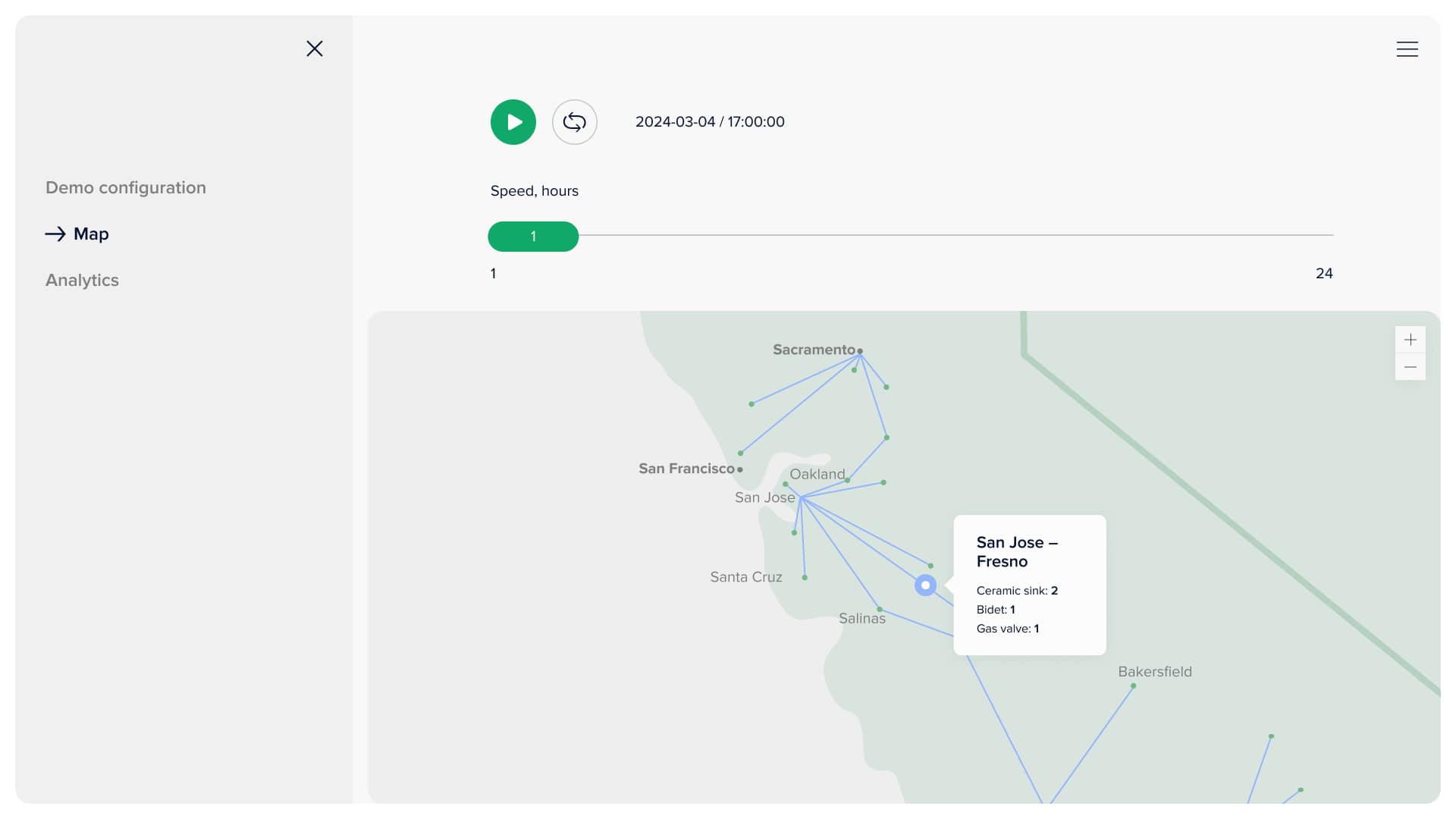
Daily deliveries to distribution points info on blue lines
Analytics page
This page features all the data and statistics about the model's proposed solution. The user can observe the delivery plan, where each ship and truck are, its estimated arrival time, route, and filling. There are also a bunch of charts, starting from the pie chart with expenses altogether and ending with heat maps of delivery costs between different seaports, warehouses, and distribution points. Additionally, the client can observe a price graph per good for different distribution points and, based on that data, make corresponding business decisions.
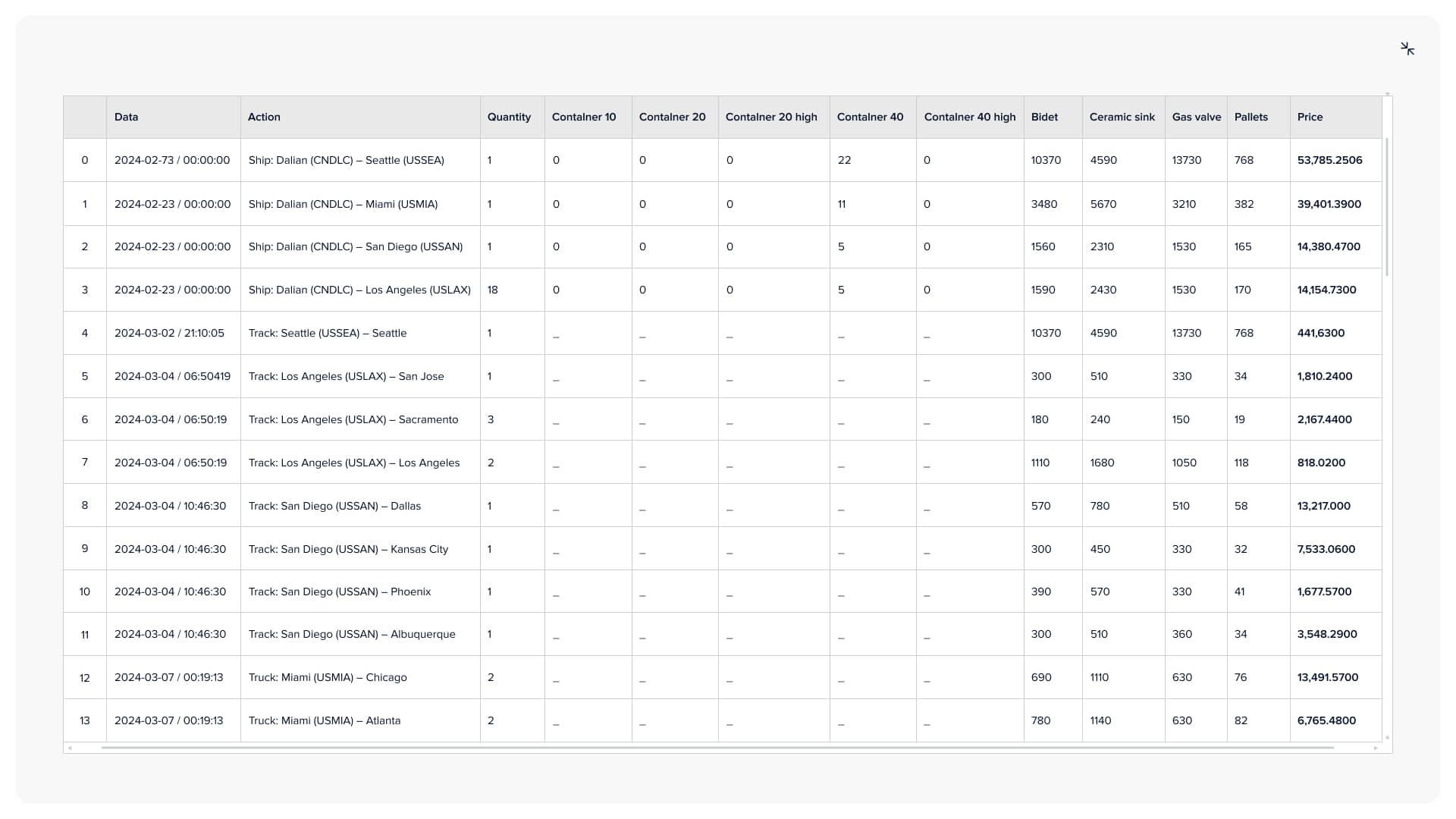
The supply chain schedule
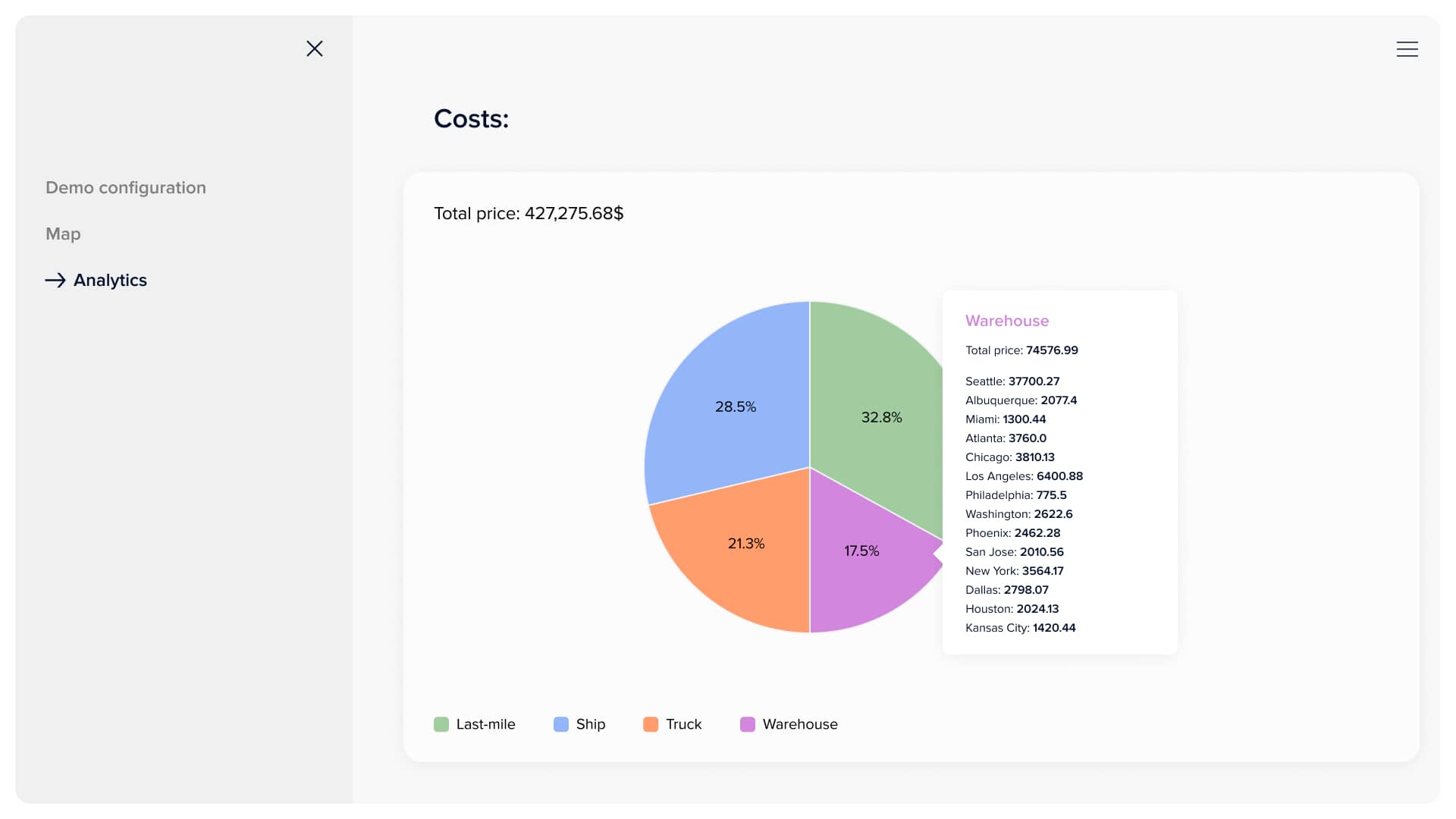
Total expenses pie chart
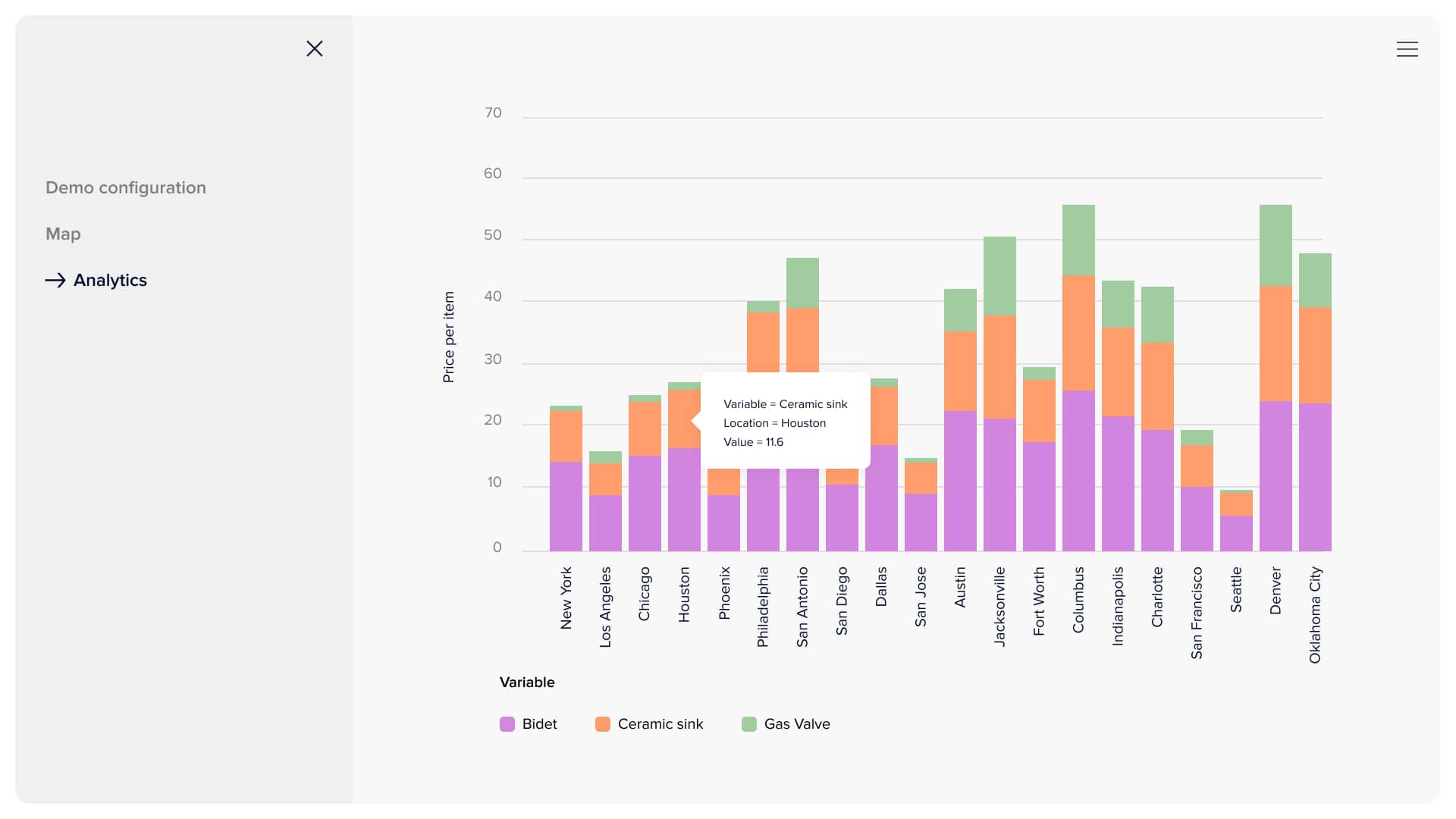
Price of delivery per good for different distribution points
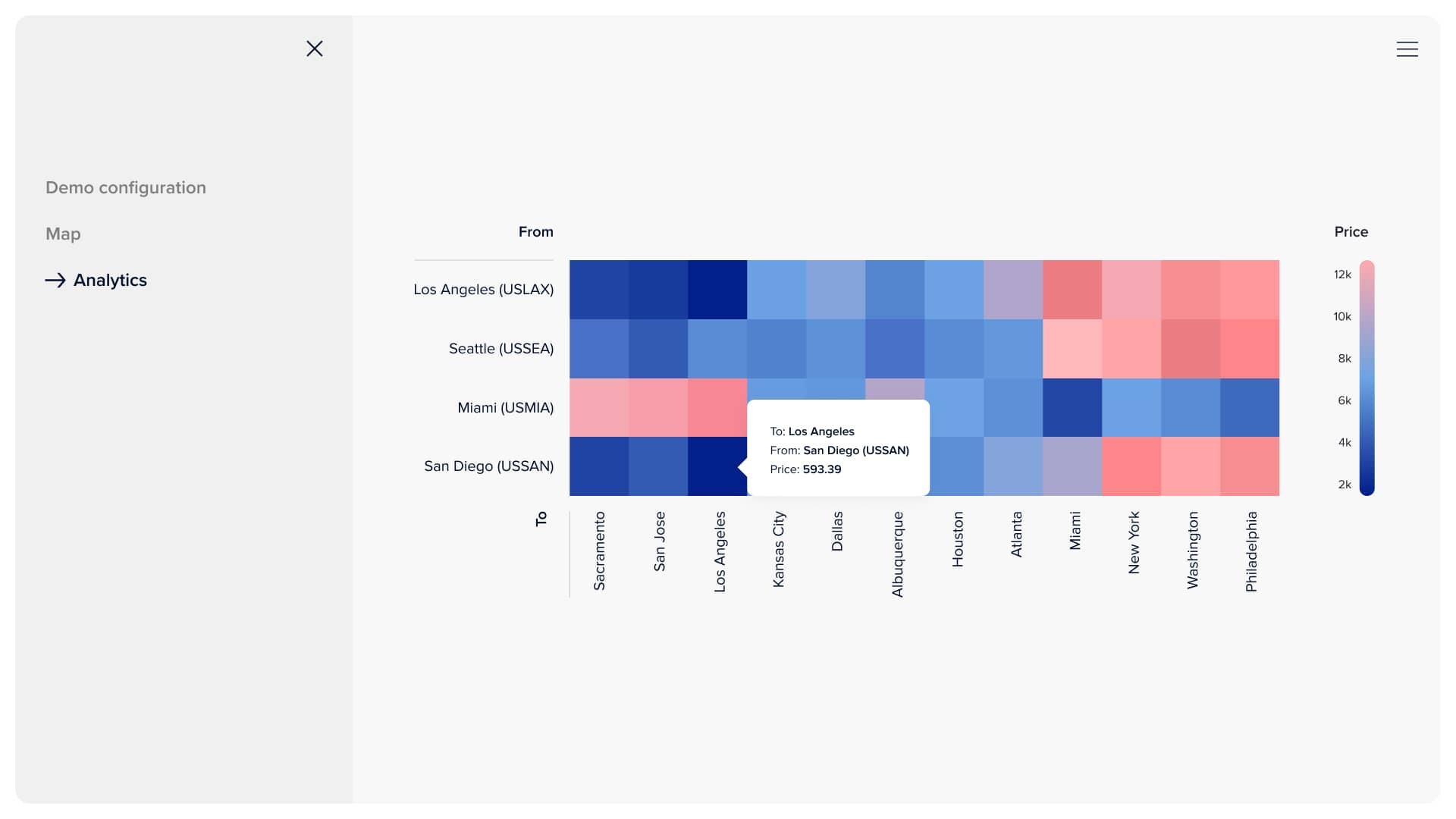
Costs for delivery from seaport to warehouses
Performance metrics: ELEKS’ solution vs client’s legacy system
The next challenge was to test our solution in real-world scenarios and compare it to the client's approach. For this purpose, the client considered a period of 1 month. The main conditions of the task (such as available seaports, location and number of warehouses and clusters) are observed in the illustrations in the previous paragraphs. As a result, our model's solution was more effective regarding operating expenses, average time of last-mile delivery, and reduced idle time of warehouses.
The data indicates that the utilization of our solution proved to be more advantageous for the client, resulting in a reduction in the price per item. This outcome can be attributed to various factors, with the primary ones being as follows:
- More intelligent goods distribution
- More optimal delivery network
- More efficient routing and warehousing
For example, our solution featured some clusters for which the model suggests last-mile delivery for different goods from distinct warehouses (an explanation lies deeply in the delivery network, and our model spotted this optimisation possibility). The distribution of goods between warehouses differed (mainly between warehouses in Washington and New York). At first sight, the differences are not so significant, but the result speaks for itself.
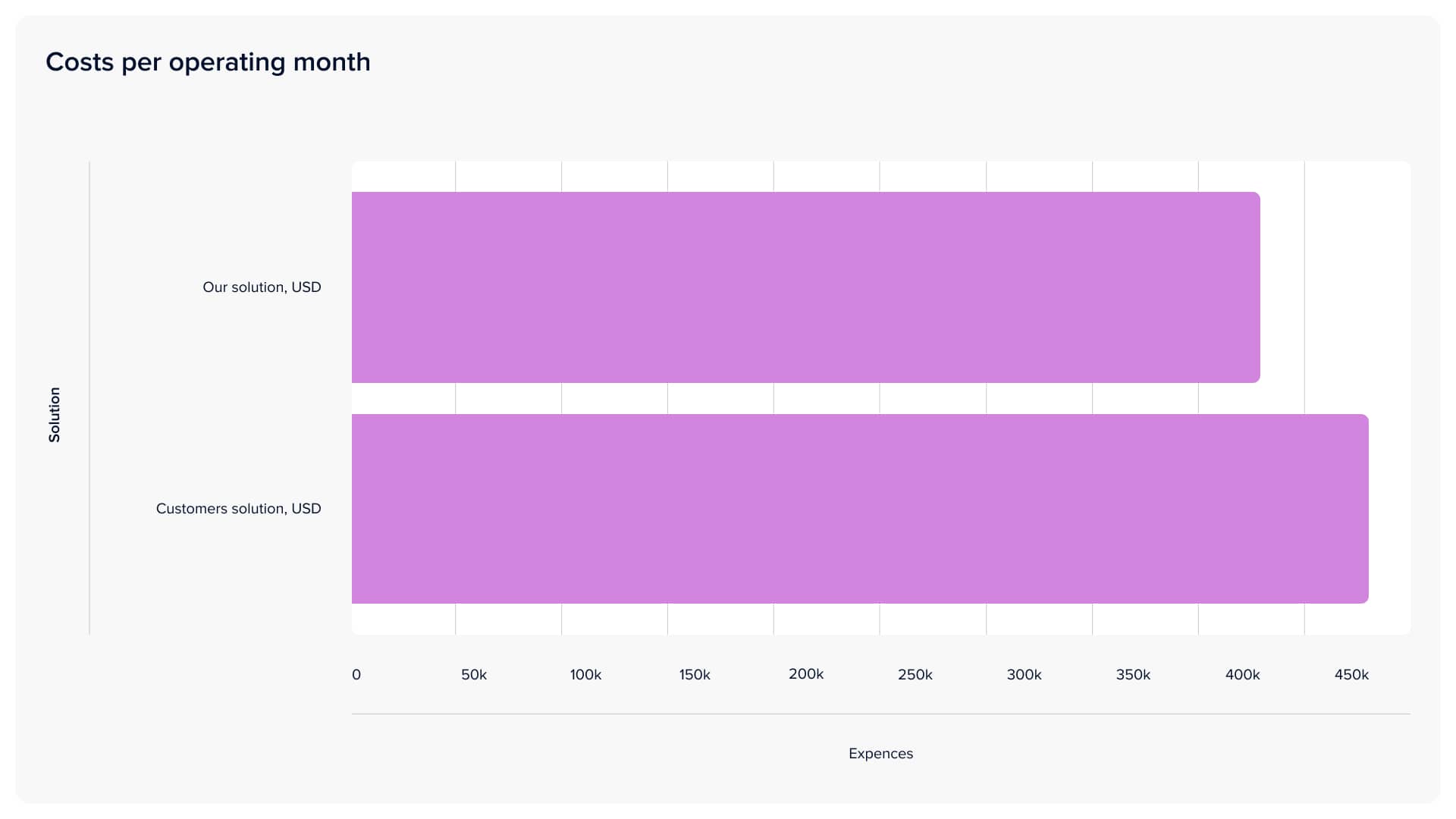
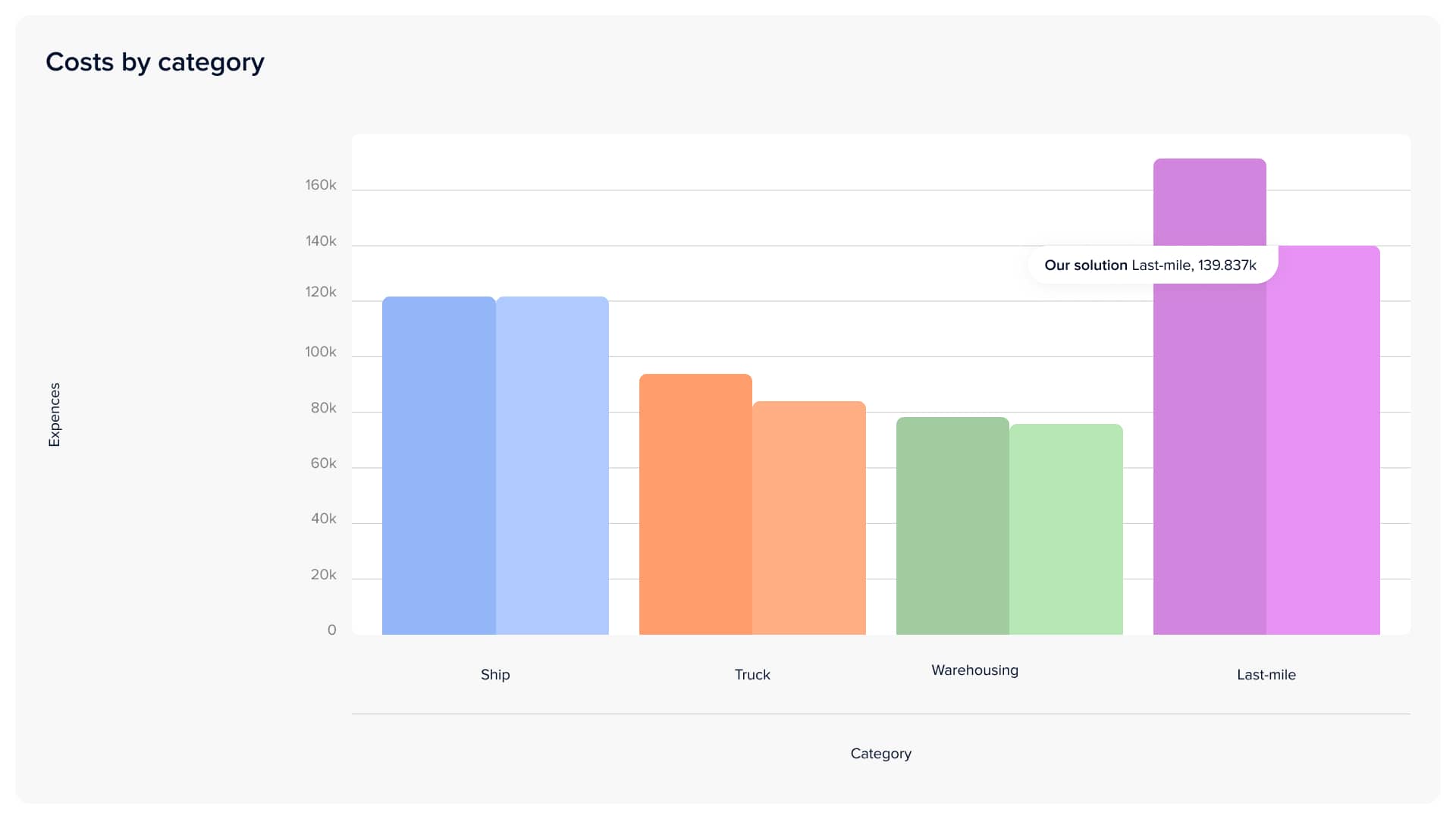
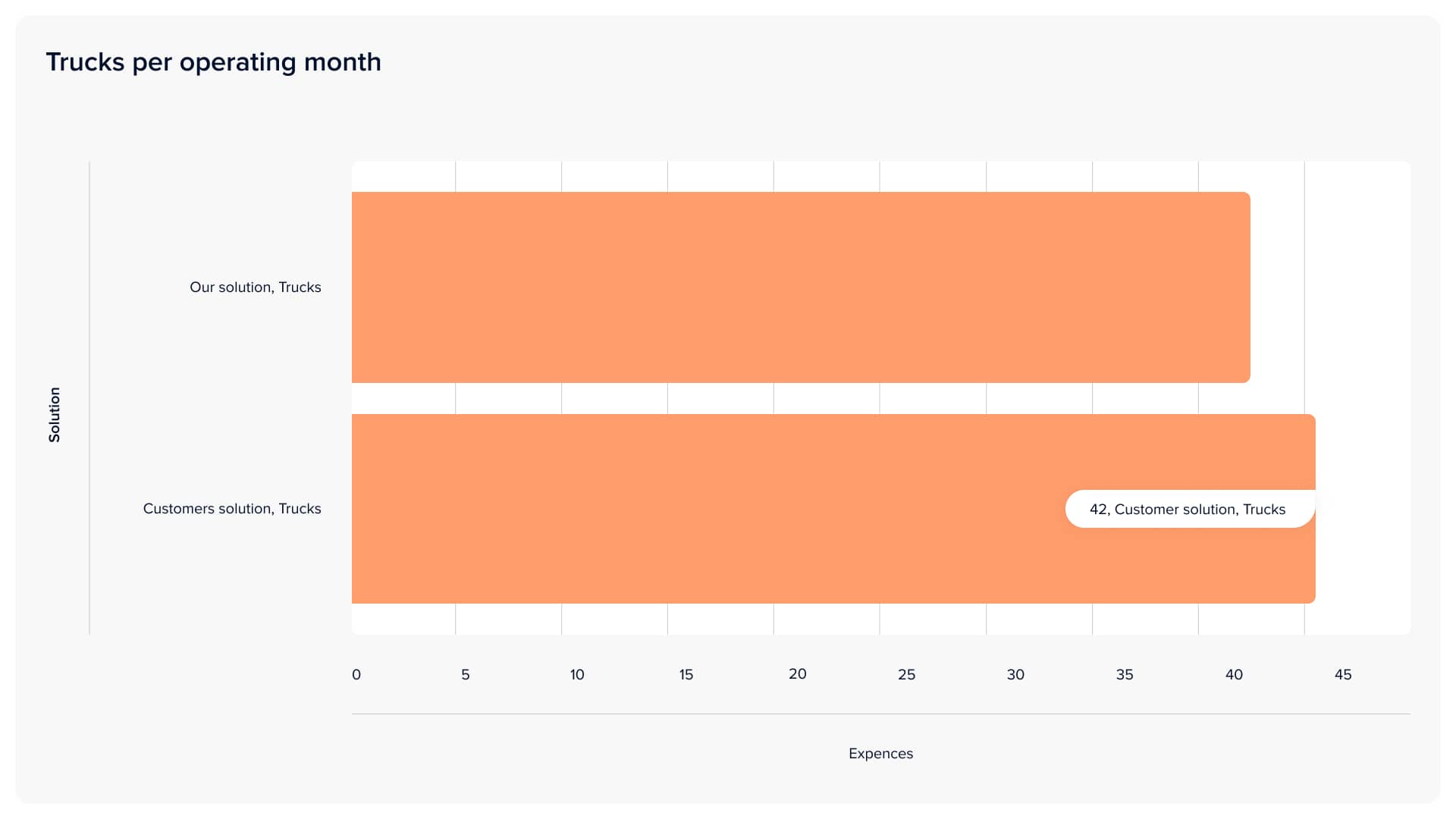
Conclusions
The integration of artificial intelligence (AI) in supply chain management emerges as a critical component for businesses aiming to navigate the complexities of global logistics effectively. The multifaceted nature of modern supply chains, coupled with challenges such as disruptions, geopolitical tensions, and economic fluctuations, necessitates innovative solutions for achieving efficiency and resilience.
The presented solution highlights AI's transformative role in streamlining supply chain managers' responsibilities and demonstrates the tangible benefits of AI and IP in supply chain logistics, showcasing a 5.76% average monthly cost savings, a 50% reduction in delivery time for some clusters. Its adaptability allows seamless adjustments, offering users access to a simulation studio, where they can execute various scenarios involving diverse items and quantities, facilitating a comparative analysis to determine optimal strategies for different situations.
To schedule a demo of this transformative solution firsthand and explore its capabilities further, reach out to us.
By ELEKS Data Science Office.

FAQs
AI in the supply chain can be used to obtain insights into inventory, shipments, and disruptions, predict disruptions based on historical data and external factors, forecast demand, streamline route planning, etc.
AI optimisation processes contribute to reducing waste, minimising energy consumption, and optimising fuel usage, fostering a more sustainable supply chain.
Generative AI is pivotal in optimising the supply chain by forecasting demand, enhancing inventory management, and improving logistics through data-driven decision-making. Its applications include demand prediction models, and route optimisation algorithms, ultimately fostering efficiency and reducing operational costs in the supply chain industry.
Related Insights








The breadth of knowledge and understanding that ELEKS has within its walls allows us to leverage that expertise to make superior deliverables for our customers. When you work with ELEKS, you are working with the top 1% of the aptitude and engineering excellence of the whole country.

Right from the start, we really liked ELEKS’ commitment and engagement. They came to us with their best people to try to understand our context, our business idea, and developed the first prototype with us. They were very professional and very customer oriented. I think, without ELEKS it probably would not have been possible to have such a successful product in such a short period of time.

ELEKS has been involved in the development of a number of our consumer-facing websites and mobile applications that allow our customers to easily track their shipments, get the information they need as well as stay in touch with us. We’ve appreciated the level of ELEKS’ expertise, responsiveness and attention to details.

